Present Value - Future Value Amortization Schedule
By now most Americans and Canadians realize the US Banks and Wall Street executives (average salary $361,000 per year) are doing well, while the rest of us unwashed are making do with the crumbs from the table. Most of the media especially journalists with common sense ( a rare trait these days) have made us aware of the US Banker’s greed, misinformation and their Wall Street cohorts. However a few issues regarding banking have always managed to stay under the radar screen.

Banking interest calculations are not as sexy topic because most North Americans are not well versed in mathematics so we naturally avoid the topic. So please bear with me, I might just save you some money! My usual advice used to be … if you borrow money demand an amortization schedule and just look at the very first payment line. I have NOW revised my advice thanx to a savvy lawyer who is a user of my software, who brought to my attention a different way that exact day interest factors can be calculated, that is by prorating interest calculations using an “exact day method”. NOW, .. my new advice is … Get the first year of an amortization schedule and analyze the first 12 lines of the schedule.
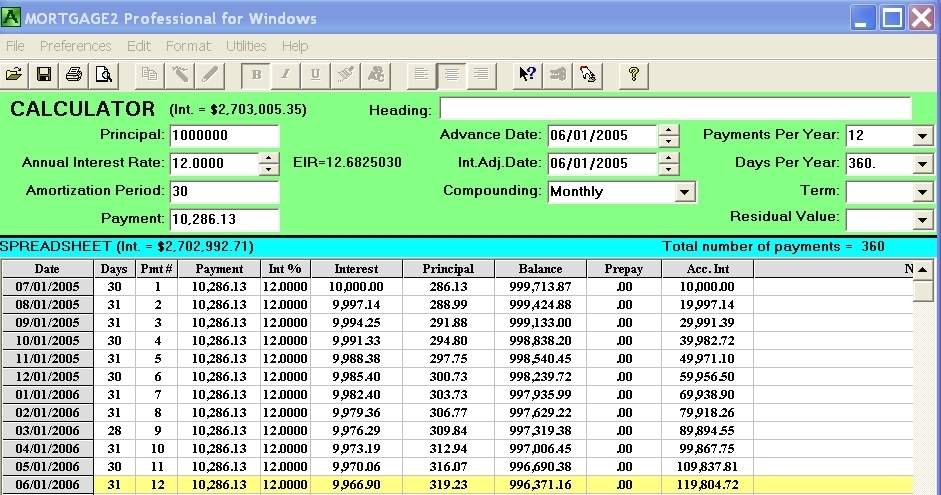
You must determine if the interest factor (which is used at the end of each month to calculate the interest owing on the outstanding balance) is constant for every line of the schedule or is it changing each month. If it is constant, the ratio of the interest portion of the blended payment to the prior months balance is the same each month right to the end of the schedule below. That can easily be seen in my example schedule because I purposely chose 12% per year which is 1% per month for a “monthly compounding” schedule. That constant monthly interest factor is 0.01000000000
If the monthly interest factor is changing each month then an opportunity exists for a lender to receive a greater than “normal” amount of interest. There is no right or wrong answer. The only legal question is whether a particular interest calculation complies with the regional or Federal laws. For example a traditional Canadian mortgage must utilize “semi-annual compounding” which is just a fancy way or indirect way of specifying how the monthly interest factor is calculated. If you waive your right to a traditional mortgage then a contract is a contract is a contract! It is hard to show sympathy for a borrower who whines after the fact because they should have had a real estate lawyer read the fine print. It is too late once the contract is signed, so it is wise to question the lender before you agree to their method of exact day interest calculations. The following example will prove my point.
As an EXAMPLE (image above) image above, I chose what is considered the normal way or defacto standard (aka Bankers year, 360 days) of computing an amortization schedule based upon algebraic equations. A principal of one million dollars, amortized for 30 years, at a rate of 12% per year utilizing “monthly compounding” which covers the majority of USA mortgages and Canadian non collateral mortgages. All financial calculators will spit out the same monthly payment of $10,286.13 regardless of the advance date. June 1st was chosen as the advance date.
The interest portion of the very first blended payment will be exactly $10,000. The interest portion of the second payment for what I call a “360 prorated calculation’ is as follows;
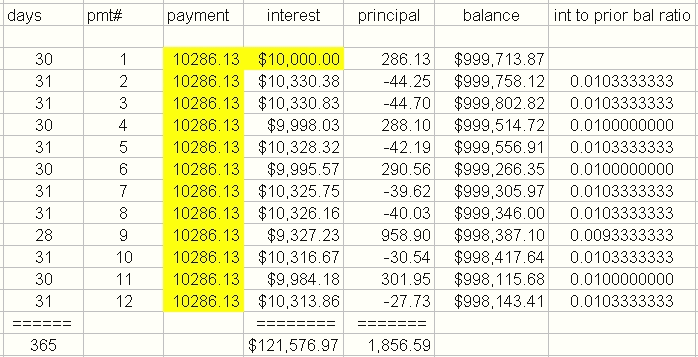
999,713.87 x (31/360) x .12 = 10,330.38
which is greater than the normal value of $9,997.14.
The prorating factor of 31/360 is because of the 31 day month. Financial calculators because of the algebra imply the year has 12 months with 30.416666 days per month (365/12=30.416666). The algebra basically divides the year into twelve equal parts. If one wanted to be real exact then the number 360 in the prorating factor should be 365 or better still 365.25
You can decide which interest calculation method you would rather pay, by comparing the following interest paid after one year.
Regular 360 Bankers year $119,805
Algebraic 365 exact day $119,817
360 prorate exact day $121,577
365 prorate exact day $119,970
365.25 prorate exact day $119,890
After one year it is obvious the 360 pro rated method give the lender the most interest out of the 5 methods outlined.
The disadvantage of the 3 prorated exact day methods is the cost of borrowing legislation in Canada and the USA will not make you aware of this situation if you don’t have an amortization schedule.
