Excessive Interest Rates
Excessive Interest Rates
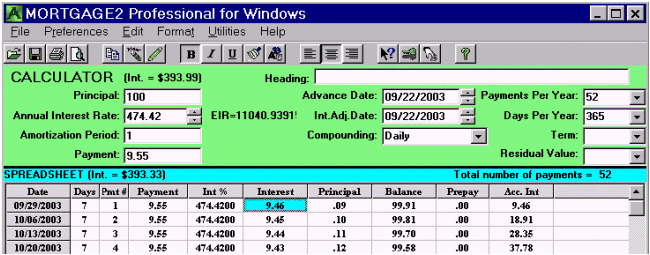
QUESTION: If someone charged you $9.46 cents in interest to borrow $100 for one week would you be able to calculate the annual interest rate or the effective interest rate the lender was using? Obviously you are able to recognize that $9.46 is excessive interest. Could you calculate the interest rate and see if it was greater than the Canadian criminal rate of 60%? You could ask your accountant to do the calculation. What if you do not have an accountant. The following example will demonstrate that apparently some lenders do not know exactly what interest rates they are charging, so don’t feel bad. Here is how you can calculate the interest rate charged in that example. Actually there is an upset consumer suing a credit card company for just that reason. The credit card company according to this newspaper article does not appears to know the interest rate they are charging. If you know an accountant or you know how to use a financial calculator then arriving at the answer is easy!

First of all, one must understand the following five definitions before delving into the example. See the definitions in detail.
Excessive Interest Rate Definintions
Annual interest rate (AIR)
Effective interest rate (EIR)
Compounding
Present value (PV)
Future Value (FV)
The AIR is the number most often quoted in the newspaper. It is often called the nominal interest rate when the compounding frequency is quoted along with it. In the USA its often and incorrectly called the APR. The APR, by definition, is the new AIR once all the costs of the loan or mortgage are factored in and it is therefore higher than the AIR.
The EIR is the same as the AIR only when the compounding is “annual compounding”. If the compounding is more frequent than annual compounding then there is an EIR associated with every AIR. As the compounding becomes more frequent the EIR increases. An AIR of 12 % with monthly compounding has an EIR of 12.6825% whereas the EIR is 12.7474% with daily compounding. Strictly speaking, “a 12% mortgage with monthly compounding” does not mean your mortgage interest is compounded monthly. What it really means is that if you miss your monthly payment the interest is compounded monthly. The incorrect nomenclature is so deeply rooted in the Canadian and American financial industry it seems impossible to correct the sloppy vernacular.
The Present Value and Future Value are exactly related by a mathematical equation over a stated period of time. If the period of time is years, then the interest rate from the equation is the interest rate for the year and by definition that is called the effective interest rate, EIR. Time and money are exactly related and Einstein referred to this as the 8th wonder of the world.
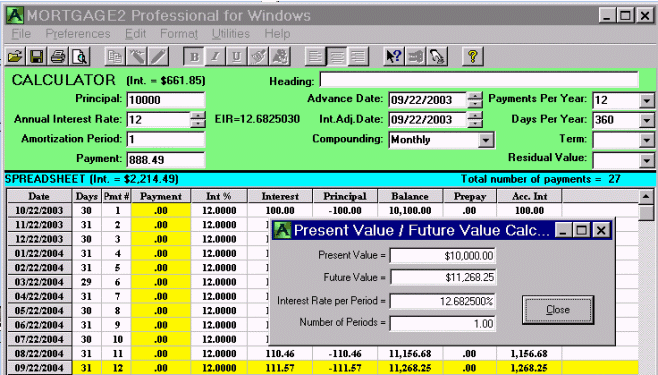
If you borrow $10,000 at 12% for one year and the lender is using monthly compounding then the monthly payments as per the calculator (green) would be $888.49. If you decided not to make payments then the interest is compounded monthly and added to the outstanding balance. At the end of one year you owe the lender $11,268.25 as shown by the negative amortization schedule. Notice how the PV/FV calculation shows the same EIR as the green calculator. In other words the Principal in the green calculator is the PV and line 12 of the negative amortization schedule is the FV. By adding 1.0 to the decimal EIR (1.0 + 0.126825) and multiplying it by the initial Principal (PV) the FV of $11,268.25 is obtained. The effective interest rate is the true rate a lender can theoretically yield because it is based upon the premise that the lender reinvests your monthly payments as he receives them each month.
Lets do a “PV/FV” calculation on the example from the newspaper article above.
Lets not split hairs and fall into the semantics trap. The borrower has to pay back the $100 plus $0.46 in “interest” plus $1.50 as a “transaction fee” plus a “transaction fee interest rate” of $7.50 for a total of $109.46
The bottom line, a borrower has borrowed $100 and has to pay back $109.46 after 7 days.

Enter PV= $100
Enter FV = $109.46
Enter n = 7/365 = 0.019178 years
Calculate the I% = 11,040.37% (that’s eleven thousand percent)
The calculated interest rate of 11,040% using the PV/FV calculator is actually the effective interest rate, EIR. In mortgage broker terminology in the province of Ontario its called the Total Cost of Borrowing. The nominal interest rate using daily compounding (worse case scenario) could be arrived at as follows (this is the simplest way instead of resorting to equations). Using the MORTGAGE2 PRO calculator let us assume we will borrow $100 and pay weekly payments over an amortization period of one year. We type in bigger and bigger annual interest rates (AIR) until we see that the interest portion of the very first weekly payment, in the amortization schedule is $9.46 When this happens the AIR or the nominal annual interest rate is 474.42% which translates into an EIR of 11,040%
The statement from the Bank reads the annual interest rate is 94.11%. This does not agree with either the 474% or 11,040%. This type of problem could easily be AVOIDED if all the provincial governments and the federal government were on the same page and used the same financial definitions and terminology.