Credit Card Late Charges
If you have been even one day late paying your credit card balance you may find this an interesting read. If a credit card’s interest rate is “excessive” the credit card lender runs the risk, of non compliance with the Federal Criminal Interest Act. The Act refers to a number of 60% but is vague on whether that is the nominal rate or the effective rate. More on that later. Even a novice knows paying the balance in full when the credit card statement arrives, entails no interest charges. One of the problems with interest calculations in general is the lack of uniform, easy to undersdtand, standards. The method used for interest calculations for loans, mortgages and credit cards should be the same by all lenders everywhere in Canada, but it is not.
The confusion starts with our legal system. Lawyers are trained as wordsmiths, not mathematicians. We should not allow lawyers to draft the laws concerning interest calculations, that is an area of expertise best left to the mathematicians. Would you ask a Civil Engineer for advice about your prostate cancer diagnosis? I don’t think so. The courts in Canada are abused and confused about interest calculations because the legalese employed in current laws is confusing, convoluted and bares no resemblance to reality. Another aspect of the problem is Federal and Provincial governments will not relinquish control over their financial domains which overlap. The legislation becomes amended and more complex as time passes with each new precedent ruled or set. Lawyers are the only people that really benefit from this continuing game.
In simple English, if you borrow X dollars and pay back X +Y dollars at the end of a period of time then, Y is called the interest. It is that simple. This concept has been around since Fibonacci discovered the basics for the concept of Present Value Future value in 1202 AD. Where the lawyers fall into their own trap is in the definition (read: words!) of the word “interest”. If governments are able to (and have done so) define the variables that influence the calculation of the Annual Percentage Rate, APR, why can they not define anything that is paid as Y, as interest? Yet, we have transaction charges, loan initiation fees, billing fees, filing fees ect., ect., all being classified as non interest. This loophole is legalese and encourages confusion. This is absurdly stupid and only serves to provide employment for lawyers.
Lets get back to the lack of uniform standards. Before I give a real live credit card example (mine) I must explain Fibonacci’s famous PV/FV algebraic equation using a simple example. CAVEAT: Do not get bogged down or distracted by the misused nomenclature, “monthly compounding”. When one has a personal loan or a non collateral mortgage the words “monthly compounding” describe the ideal scenario of a lender getting a true yield by investing each monthly payment at the same interest rate as the payments are received. That is all it means. NOTE; “monthly compounding” on a loan or mortgage document, does NOT mean the interest you are being charged is compounded monthly, the same logic holds for a traditional Canadian mortgage that have the words, “semi-annual compounding, six months not in advance” added to the legal documents. The wording “semi-annual compounding” initially, probably meant to notify the borrower the lender is calculating the monthly interest factor in a certain manner. The infamous words do not mean the mortgage interest is only calculated every six month, but I digress!
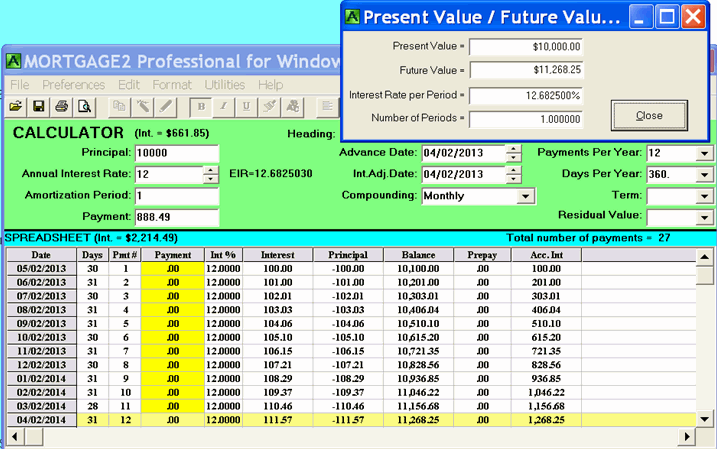
Borrowing $10,000 for one year at a rate of 12% utilizing “monthly compounding” (read: the monthly interest factor is 1%) is the example I will use. A negative amortization schedule where all payments are set to zero, generates a grid of Future Values by way of Fibonacci’s famous equation,
FV=PV (1+i)^n
where “i” is the interest factor and “n” is the number of periods. If “n” is in months then “i” is the monthly interest factor. This is one of the simplest of algebraic equations and the least understood by many people. What that equation means is, if i = .01 and n = 12 then 1.01 multiplied by itself 12 times equals 1.126825
When discussing a loan or mortgage the “i” is the monthly interest factor used to calculate the interest due at the end of each month. When discussing a savings account or an account where you deposit money each month, with the option of true monthly compounding, the “i” is the monthly interest factor that is truly generating compound interest (interest on interest). This is where the confusion starts. The expression “monthly compounding” describes how the numerical value of the interest factor is calculated and is really only informative in the case of an investment growing by compounding. BUT for some strange reason, it is always included in legal borrowing documents. You are not paying compound interest on a loan or mortgage if you make all your payments on time. You are paying simple interest.
This was a long way to travel to demonstrate that a nominal annual interest rate of 12% with “monthly compounding” is equivalent to an annual interest rate of 12.6825% with annual compounding. They both yield the same amount of money, $11,268.25 at the end of the year. In Financial circles, the annual interest rate with annual compounding is usually called the EFFECTIVE INTEREST RATE (EIR). If two loans or investments have the same EIR they are identical and therefore one does not need any further information.
To repeat, … in a mortgage or a loan, the type of compounding stated, determines the numerical value of the interest factor for a specific period of time. If the period of time is a year then an annual interest rate of 12.6825% on a $10,000 investment (PV) will be worth $11,268.25 (FV) one year in the future. If the period of time is a month then a monthly rate of 1% compounds your $10,000 investment into a value of $11,268.25 after 12 months. Fibonacci’s equation is a way of calculating the annual rate which is also usually called the EIR, which is based upon a yearly period of time. This was a long way to go in this example but it is essential in order to understand the credit card calculation to see if it exceeds the criminal interest rate. Once the proper period of time is used in the PV/FV equation, the EIR can be calculated.
The question that nobody wants to address is “the proper period of time”.
I was one day late on my credit card payment. My balance was $600.17
They charged me $14.25 for being one day late on a balance of $600.17. Looking at the period as one day the EIR I was charged was over a half a million percent. Looking at the period of one month (30 days) the EIR is 102.2% which is well over the Criminal Rate. Because I was such a good customer and I usually paid on time they credited my account for the interest charge.
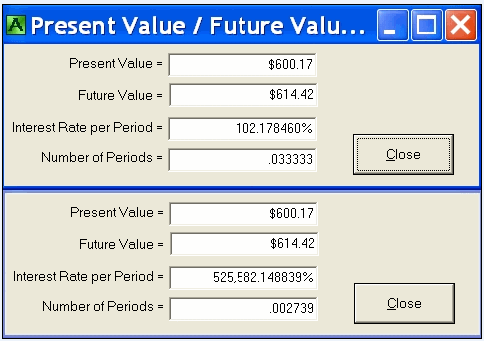
Another way of looking at this one day late examples methodology is as follows.
What if you borrowed $10,000 and at the end of the year the lender told you that you owed him $10,000 plus $1.268.25 in interest. The number of periods is one year. The PV equals $10,000. The FV equals $11,268.25
The calculated interest rate per period is 12.6825%.