Canadian Mortgage Prepayment Penalties
Banks make a profit by lending money. Banks charge interest for that service. The money they lend you is usually somebody else’s money. If a Bank is paying someone 9% for the use of their money and the Bank is lending it to you at 12%, the 3% difference is the Bank’s profit. I have no problem with that concept!
When a Bank lends you money to purchase a house, you pay them back on a monthly basis. Obviously the Bank would like to lend your monthly payment to someone else as quickly as possible at the same interest rate or higher in order to maximize their profit. Again, I have no problem with that concept.
Banks perform an ideal calculation on their mortgages called deemed reinvestment. It is assumed as each monthly payment is received a Bank will lend out your monthly payment at the same interest rate to someone else in order to achieve the effective interest rate (EIR). In reality, it’s virtually impossible to achieve this deemed reinvestment principle on every mortgage in a Bank’s portfolio.
Let us stay with this example of borrowing $1000 for one year at an annual interest rate of 12% Think of it as a very tiny mortgage amortized for one year. An annual interest rate of 12% is purposely chosen so you can easily “see” the calculations. “Monthly compounding” was purposely chosen to keep the mathematics visually simple. 12% per year is 1% per month (the monthly interest factor is 0.01 as a decimal) and the math can be seen by moving the decimal two places to the left. NOTE!!! Using “semi-annual compounding” (as is normal in a regular Canadian mortgage) the explanation would be IDENTICAL but the monthly interest factor would not be as easy to calculate or visualize (it would be 0.0097588 compared to 0.01).
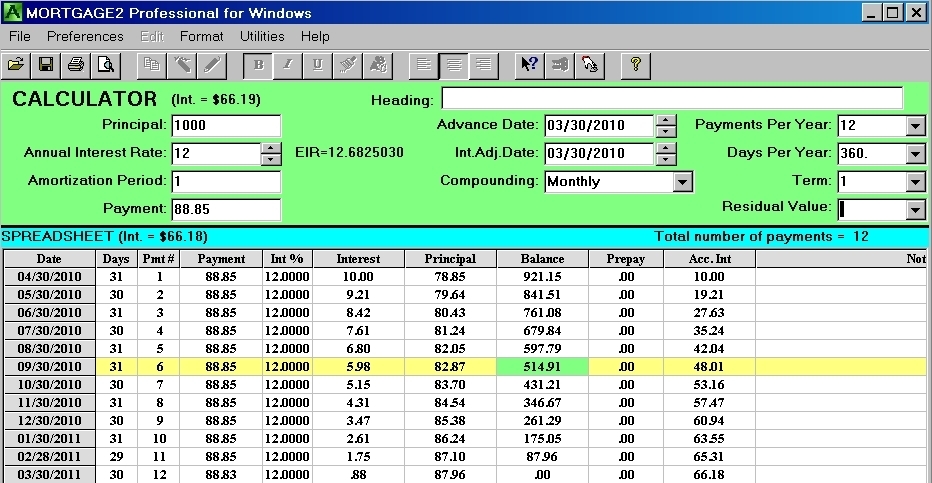
schedule A
If a Bank cannot lend your monthly payment at the same rate each month to someone else and your payment was left sitting in their vault, they would earn a total of $66.18 in interest at the end of the year (see schedule A). Yet 12% divide by 100 multiplied by $1000 is $120. At first thought you would say the Bank makes a $120 a year in interest? If the Bank could actually lend your payments each month as they are received the Bank would earn $126.83 (not $120) in interest on your $1000 loan. The extra $6.83 interest is because of the compounding, .. interest upon interest is compounding. So on a loan of $1000, if each monthly payment is lent to someone else on the day it’s received, at the end of the year the bank earns $126.83 in interest. The banks effective interest rate, EIR, of 12.6825% is achieved because of the compounding of interest if the ideal assumption of deemed reinvestment is achieved. Achieving the EIR the Bank is left with a total of $1,126.83 at the end of the year (see the negative amortization schedule in screen B below).
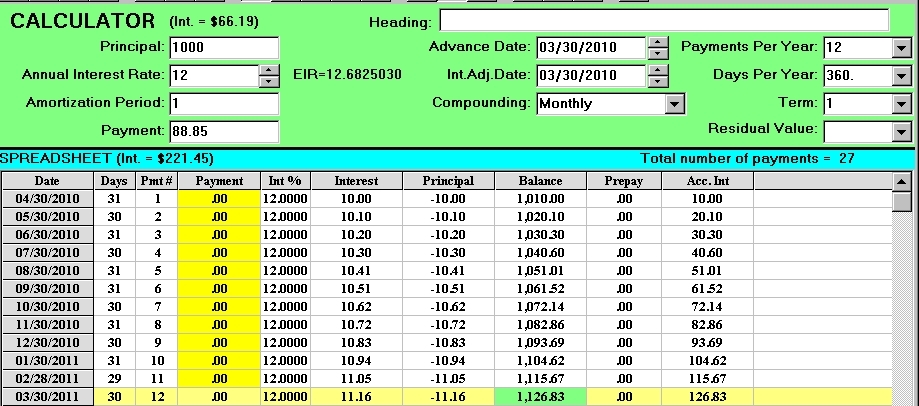
schedule B
Its interesting to note what an EIR actually tells you. Take the EIR as a decimal (.126825) and add 1.0 to it (1.126825) then multiply it by 1000 (1000 x 1.126825= 1,126.825) and that becomes the amount of money the lender receives if the deemed reinvestment criteria is met.
What happens if, in the middle of the year the market conditions dictate that a different bank offers you 6% interest for the remainder of that $1000 loan and you debate on whether to change banks for the remaining 6 months?
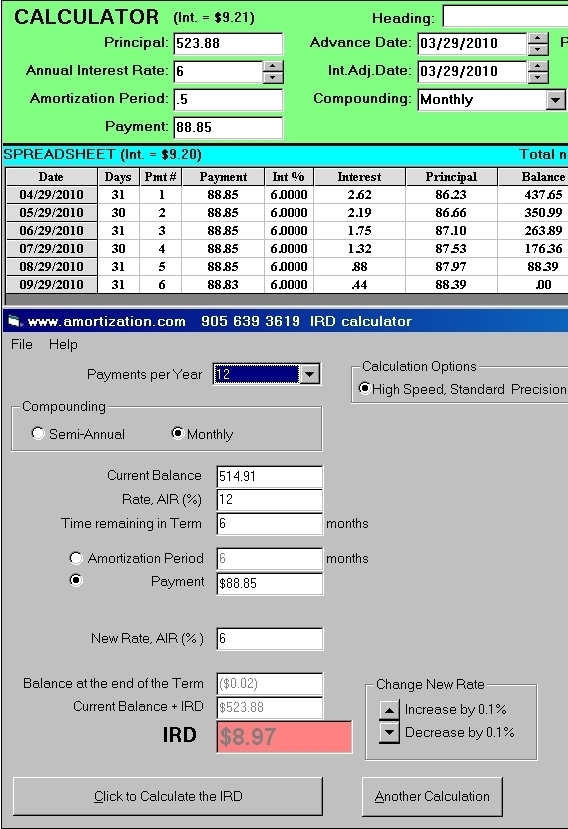
schedule D
You ask your Bank manager if he will let you terminate your one year term (in this example, your term and your amortization period are both one year) and he agrees if you pay the bank an IRD of $8.97 (see screen D). Let us assume the IRD is correct. By paying the IRD you have opened your mortgage and you can now go to the other bank after you pay your current bank $514.91 plus the $8.97 IRD “penalty” (see screen A).

schedule A
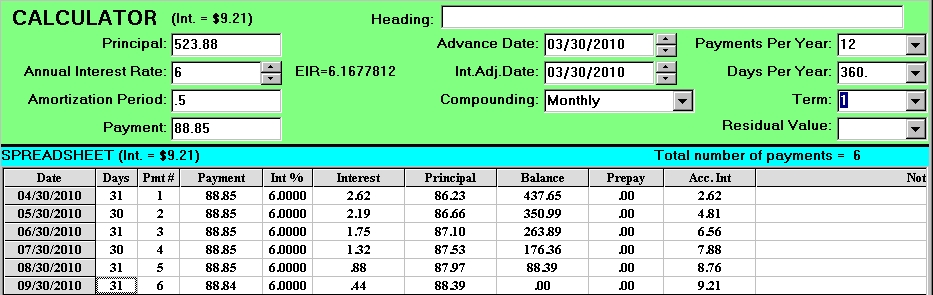
screen C
On the other hand, you can remain with your bank and pay the $8.97 IRD along with your sixth payment and continue on at 6% instead of 12% . Looking at the 6% amortization schedule (screen C) you can see that you end up paying off the mortgage in the same time frame, one year. The IRD was correct. The purpose of the IRD was to give the Bank the same cash flow (12 months of $88.85) if the IRD was paid and the rate was lowered for the remaining 6 months.
From a borrowers perspective you have two options which in reality are one in the same.
1.. Pay your current Bank the IRD and continue on with the same payments but at the lower interest rate. This would properly be called an “interest rate buydown”.
2.. Switch to the new bank. At the new Bank you are borrowing the $514.91 plus the $8.97 IRD to pay off your loan at your original bank.
The bottom line. You still end up paying 12 payments of $88.85 (except for the last payment that’s 2 cents less) and you have saved nothing no matter which choice you made. That is the purpose of the IRD, to fairly compensate the Bank. Because if, and that’s a BIG if, your original Bank really does have all your payments tied into another financial vehicle, like Bonds, the Bank needs to honour that contract. A contact is a contract! Conclusion: If the IRD is calculated correctly, and you pay it, you save nothing! You have really changed 4 quarters for a dollar.
When a Bank charges, a three month interest penalty or an IRD “penalty” which ever is greater, that is unfair and unethical to the borrower. Also, an IRD calculation based upon the difference of a new rate and the posted rate that was in effect at the time of signing is also unfair and unethical.
When signing a new mortgage often a Bank will give you a rate less than the posted rate however if it becomes necessary to do an IRD calculation some Banks use the posted rate in the IRD calculation because it gives them a larger IRD calculation. This is also unfair and unethical! I am a glass half empty type of guy. I believe the Bank sometimes gives you a lower than posted rate, not to reward you for being a good customer but to cover their backside in case you elect to pay the early renewal penalty.
Canadian banks are not low margin businesses as can easily be seen with year after year recording of multi BILLION dollar profits. There is no ethical justification for a Bank to maximize profits on the backs of average Canadians by playing games with confusing, convoluted early renewal “penalties.” The Canadian Federal Finance Minister, Honourable Jim Flaherty, announced in his February 2010, budget he was bringing in legislation to make the early renewal penalties consistent with all Canadian Lenders. The mathematics behind these IRD calculations (present value-future value) was first developed in 1202AD by Fibonacci in his “book of calculations”. It seems that there is nothing new under the Sun. Why has it taken so long for the Federal government to do the right thing?
