APR Overview
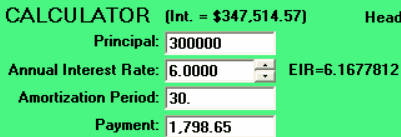
You just purchased a house for $300,000. The lender is charging you an annual interest rate of 6% and therefore the monthly payments will be $1798.65 for the next 30 years providing the rate remains at 6% for the next 30 years. The mortgage broker who arranged this deal just asked you for a cheque or cash for $3000 to cover the total of ALL the up front closing costs. The breakdown of these upfront costs is irrelevant with respect to the following mathematics. What is important is the total of these upfront costs! There is much discussion in Canada and the USA as to what costs should be considered appropriate as part of the up front costs that in turn have an impact on the actual rate of interest you are paying for the loan. The point is, costs, for example, such as ongoing monthly insurance premiums must be converted to up front costs using present value (PV) future value (FV) calculations based upon effective interest rates.
The actual rate of interest you are paying for the loan is commonly called the APR in the USA (annual percentage rate) and the TCOB in Canada (total cost of borrowing). As a side issue, every annual interest rate (AIR) has a corresponding effective interest rate (EIR) depending upon the “compounding frequency”. If the compounding frequency is annual then the AIR and EIR are identical or equivalent. The EIR is a handy number to know as it’s the only way of intelligently comparing a mortgage as an investment to a financial vehicle such as a mutual fund’s yield (the annual compounded rate of return).
On closing day, the bank “hands you” $300,000. You give the mortgage broker $3000 and yet you will be paying monthly payments to the bank based upon $300,000 when in essence your net cash on hand is $297,000.
Using the www.amortization.com calculator, or any other financial calculator that has this feature, change the Principal to $297,000 and recalculate the annual interest rate in order to pay $1,798.65 for the next 30 years.
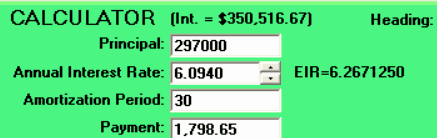
The newly calculated annual interest rate is 6.0940% and its corresponding effective interest rate is 6.2671% (because of “monthly compounding”).
The words “monthly compounding” actually refer to the situation of how the interest is compounded if a payment is missed. If a monthly payment is missed the interest due is added to the outstanding balance and next months interest calculation is based upon an outstanding balance that contains unpaid interest. By definition, monthly compounded interest. If the schedules monthly payments are made in full each month, the interest calculated is not monthly compounded. The monthly compounding only refers to the case when the payments are missed. The words “monthly compounding” really should be replaced by “monthly compounding of interest if payments are missed”. The esoteric and confusing vernacular is so strongly imbedded in the financial industry it is almost impossible to clarify.
To reiterate, the percentage number, 6.0940% in the USA is called the APR. The percentage number, 6.2671% in Canada is called the TCOB.
In summary; this mortgage and its real interest costs are the same whether you quote the AIR or the TCOB. The American technique is a “six pack” and the Canadian technique is a “half dozen”. It does not matter which percentage number is used as long everyone understands and uses the same calculation procedures. The example just cited, it was assumed the borrower had the upfront closing costs in cash or a cheque from a separate savings account.
If you have to borrow the upfront costs from the lender, the calculations are as follows. The $3000 is added to the mortgage and the monthly payments ($1,816.64) are calculated based upon the $303,000. Then the new AIR (6.0931%) is calculated based upon $300,000 loan with payments that were based upon $303,000
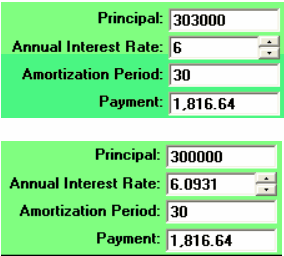
The APR for this scenario, is 6.0931%. At two decimal places (6.09%) one cannot see the difference in the two calculation scenario procedures. One should at least be aware of the two different situations. Also be aware that in order to compare the APRs of mortgages, the mortgages must all have the same amortization periods.
Regardless of which method being employed (because of the different circumstances, …borrowing the upfront costs vs having the cash on hand) it should be noted, if the up front costs are considered over a shorter period of time (term) other than the amortization period, the corresponding numbers are larger and much more difficult to calculate. For those calculations you must be very proficient at mathematics or else use software such as the Discounting module found in the UTILITIES menu of MORTGAGE2 PRO software.
