An Inconvenient Mortgage
If the interest rate for a loan was quoted as an effective interest rate (EIR) there would be less confusion in loan shopping! The EIR is the actual interest rate you would pay yourself at the end of the year if you lent the money to yourself. You are borrowing the money from a lender and it is assumed that the lender re-lends your payments out as he receives them at the same interest rate. Its an ideal calculation however it’s a consistent reference point for comparing loans. You would not need to be concerned with the inconvenience of compounding!
Before you can understand the advantage of using the EIR, you must understand the meaning of the word, “compounding”. Compounding does not mean calculation! If you make all loan payments on time the interest you pay on your loan is not compounded!
As a related issue, the mathematical formulas, calculations and analysis of mortgages and loans are identical. The difference between a mortgage and a loan in Canada is the numerical value of the interest factor that is used to calculate interest due at the end of the payment period. The type of compounding utilized influences the numerical value of the interest factor. A Canadian mortgage is a specific name for a loan that utilizes semi-annual compounding. From this point on, only the word loan will be used throughout the discussion.
This story could have happened 100 years ago. A farmer borrowed $1000 to purchase seeds to plant a crop. Most loans to farmers then were on a six month basis. The farmer agreed to pay back the $1000 loan plus interest after 6 months. The lender told him the annual interest rate was 12%. They both agreed and parted ways.
Six months later, the farmer’s car broke down on the way to the bank to pay back his loan. The banker tells the farmer he owes the $1000 plus $60 in interest. The farmer asked his banker if he could continue the loan and not pay ANY money on the loan for another six months, because his car needed repairing. The banker agreed.
6% for 6 months is 0.06 as a decimal
0.06 x $1000 = $60
If the farmer had the money he would have paid the banker the $1000 principal he borrowed plus the $60 in interest for a total of $1060.
The 0.06 is the interest factor
The period of time is six months
SIX MONTHS LATER
A full year has elapsed now. The farmer returns to his banker to pay back the loan in full. His crop was a bumper crop (nothing to do with the repaired car) and the farmer was in good financial shape.
The banker tells the farmer he owes $1060 for the first six months plus $63.60 in interest on the $1060 for the last six months.
$1060 x .06 = $63.60
In total now after one year, the farmer owes $1,123.60
$1000 + 60 + 63.60 = $1,123.60
The interest of $63.60 by definition, is compounded interest because it is interest calculated on interest for the second six month period of time.
Note: 1.06 x 1.06 x 1000 = $1,123.60
On the basis of one year the banker receives $123.60 of interest.
(123.60/1000)x 100 = 12.36%
The interest rate initially agreed upon was 12%. But because the way the calculations were done at the end of each time period, the effective interest rate (EIR) is 12.36% In financial circles the effective interest rate is always based upon a one year period. Adding the word “annual” in front of words “effective interest rate” is redundant and confusing because it implies there are other effective interest rates for shorter time periods. In fact doing a present value Future value calculation on all financial calculators requires one to know the EIR for the yearly period of time. Also knowing the EIR allows one to calculate a bottom line regarding an investment each year by adding 1.0 to the EIR as a decimal and multiplying the initial balance at the beginning of the year; as follows
12.36% is decimal 0.1236
1.1236 x 1000 = 1,123.6
The interest was calculated semi-annually or in other words at the end of the first six month period and at the end of the second six month period of time the interest was again calculated (semi-annually) but this time the interest was compounded.
100 years into the future, today.
The same farmer needs to borrow $1000 but is now willing to pay back the loan with monthly payments but wants an effective interest rate of 12.36%.
Interest calculations will be done at the end of each monthly period and monthly payments will be made at the end of each monthly period. Notice the emphasis “at the end of each period”, because nobody pays interest payments in advance.
In this example the period of time is one month and the monthly interest factor would naturally be 0.12/12 = 0.01
HOWEVER, if the farmer wants the EIR to be 12.36%, then mathematically speaking, 1.0 plus a particular monthly interest factor multiplied by itself 12 times must equal 1.1236
How this particular monthly interest factor, 0.0097588 was calculated is not important at this point in the explanation. What is important is for the EIR to be 12.36% then
(1.0097588 ) ^ 12 = 1.1236
The symbol “^” means that the contents of the brackets are multiplied by itself 12 times.
If the twelve monthly payments were missed the interest owing is calculated at the end of each month, and added to the initial principal, as shown below, the initial $1000 loan would grow to $1,123.60 thus an EIR of 12.36%
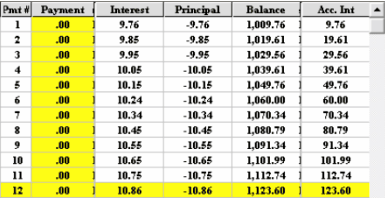
The theory is as follows. It is assumed the lender immediately lends out your monthly payments as he receives them (legalese .. deemed reinvestment)
in order to achieve the interest of $123.60 which translates into a 12.36% EIR .
The amortization schedule below shows, if the lender did not reinvest each payment as he received them, at the end of the year he would only have received $64.56 in interest.
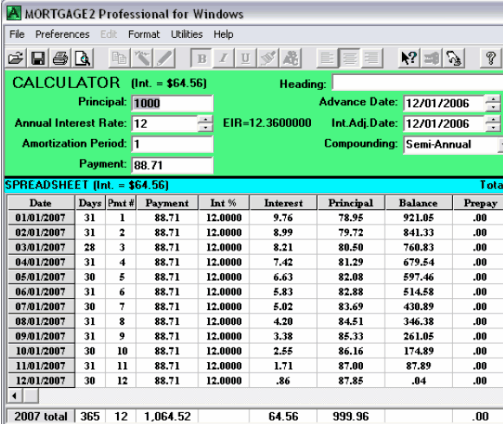
Notice that in both examples interest calculations are made at the end of each time period but the monthly payment mortgage’s interest factor allowed the lender to achieve the same EIR as if the payments and calculations were done every six months.
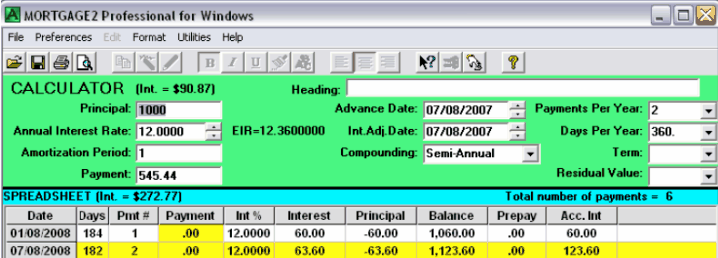
The standard Canadian legalese is as follows.
“Blended monthly payments with a nominal interest rate of 12%, compounded semi-annually, not in advance “
This wording confuses people. The points below should help in understanding your mortgage documents.
The ten commandments of Interest!
1.. Compound interest is interest paid on principal plus unpaid interest.
2.. When the payment frequency and compounding frequency are the same the interest factor for that payment frequency is the nominal rate divided by the payment frequency.
Most US mortgages and personal loans in Canada and the United States quote a nominal rate with monthly payments and monthly compounding. For example a 12% nominal rate translates into a monthly interest factor of 0.01 (.12/12) and an EIR of 12.6825% ( (1.01)^12 = 1.126825 ).
3.. Compounding and calculation are different words and mean different things.
4.. Interest calculations are done at the end of the payment period and then a payment is made.
5.. Interest calculations are not made in advance. Interest is the cost of using the lenders money for a given period of time, paid at the end of the time period.
6.. The only way a loan could have interest compounded (compound interest) is when a payment is missed and the missed interest portion of the payment is added to the outstanding balance. So if only one payment is missed, then from that point on the loan has compounded interest.
7.. Interest for the lender is compounded when he reinvests each payment back out on the street at the same interest rate he is charging you.
8.. The reference to the compounding method in loan documents only serves to define the interest factor and unfortunately confuses the novice borrower.
9.. The EIR is calculated by adding 1.0 to the interest factor for the payment period and then multiplying it by itself by the number of payment periods per year.
For example;
Canadian Mortgage
A monthly payment mortgage
A nominal rate of 12%, semi-annual compounding
(Annual Interest Rate, AIR = 12 in the MORTGAGE2 PRO calculator)
Interest factor = .0097588
EIR = (1.0097588)^12 = 1.1236 which is 12.36%
American Mortgage
A monthly payment mortgage (or a personal loan)
A nominal rate of 12%, monthly compounding
Interest factor =0.12/12=0.01
EIR = (1.01)^12 = 1.126825 which is 12.6825%
10.. When the payment frequency and the compounding frequency are NOT THE SAME you cannot divide the nominal rate by the payment frequency to arrive at the interest factor. For Example;
Canadian Mortgage
A monthly payment mortgage
A nominal rate (R) of 12%, semi-annual compounding
Payment frequency = monthly
Compounding frequency = semi-annual
Monthly interest factor = i
i does not equal .12/12
rather
i = ((1+R /2)^(1/6)) – 1 = 0.0097588
EIR = (1.0097588)^12 = 1.1236 which is 12.36%
The advantage of using the EIR in comparing loans, (even though it is the theoretical rate the lender achieves using your money), is if two loans have identical EIRs for the same principal and payment schedule then it matters not which lender you go with, all else being equal. The equivalent nominal interest rate is when two mortgages because of the different compounding method have the same EIR. The two amortization schedules would be identical as they should be. Notice below, at four decimal places the calculator shows that 11.7106% with monthly compounding and monthly payments is equivalent to 12% with semi-annual compounding and monthly payments. The simplicity of stating the EIR for all loans eliminates the chance of compounding confusion for most people (pun intended).
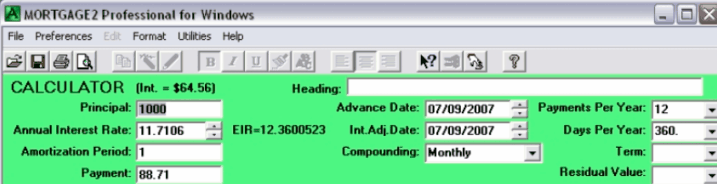
Its appropriate to note, the basis of the new Ontario “cost of borrowing” legislation (which used to be called the “Total Cost of Borrowing”) is that once all the fees and costs for a loan have been factored into the calculations the new (and larger) EIR is quoted as a percentage as the COST OF BORROWING.
When lenders quote different nominal rates at different compounding frequencies they are banking on the fact (no pun intended) that your novice status as a mathematician will work in THEIR favour!
